Compute Divisors for Positive Integers
Use the form below to get the divisors of and additional information about any positive integer up to 1 million. (decimal places are rounded)
Or just append the integer you want information about to the end of this site's URL. e.g., www.positiveintegers.org/5
The Integers 1 to 10000
- Range is a range of numbers, in groups of 100. Click on the range for more information about that range.
- Count(Primes) is the count of Prime Numbers in that range.
- Count(Fibonacci) is the count of Fibonacci Numbers in that range.
- Max(Count(d(N))) is the highest number of divisors that any single number within that range possesses.
- Most Composite N is the list of the numbers in the range that have the most divisors.
- Count(Deficient), Count(Abundant), and Count(Perfect) are the counts of Deficient, Abundant, and Perfect numbers in that range.
| Range | Count(Primes) | Count(Fibonacci) | Max(Count(d(N))) | Most Composite N | Count(Deficient) | Count(Abundant) | Count(Perfect) |
|---|---|---|---|---|---|---|---|
| 1-100 | 25 | 10 | 12 | 60, 72, 84, 90, 96 | 76 | 22 | 2 |
| 101-200 | 21 | 1 | 18 | 180 | 76 | 24 | 0 |
| 201-300 | 16 | 1 | 20 | 240 | 77 | 23 | 0 |
| 301-400 | 16 | 1 | 24 | 360 | 73 | 27 | 0 |
| 401-500 | 17 | 0 | 24 | 420, 480 | 74 | 25 | 1 |
| 501-600 | 14 | 0 | 24 | 504, 540, 600 | 76 | 24 | 0 |
| 601-700 | 16 | 1 | 24 | 630, 660, 672 | 76 | 24 | 0 |
| 701-800 | 14 | 0 | 30 | 720 | 74 | 26 | 0 |
| 801-900 | 15 | 0 | 32 | 840 | 75 | 25 | 0 |
| 901-1000 | 14 | 1 | 28 | 960 | 74 | 26 | 0 |
| 1001-1100 | 16 | 0 | 32 | 1080 | 77 | 23 | 0 |
| 1101-1200 | 12 | 0 | 30 | 1200 | 76 | 24 | 0 |
| 1201-1300 | 15 | 0 | 36 | 1260 | 76 | 24 | 0 |
| 1301-1400 | 11 | 0 | 32 | 1320 | 74 | 26 | 0 |
| 1401-1500 | 17 | 0 | 36 | 1440 | 74 | 26 | 0 |
| 1501-1600 | 12 | 1 | 32 | 1512, 1560 | 77 | 23 | 0 |
| 1601-1700 | 15 | 0 | 40 | 1680 | 74 | 26 | 0 |
| 1701-1800 | 12 | 0 | 36 | 1800 | 75 | 25 | 0 |
| 1801-1900 | 12 | 0 | 32 | 1848, 1890 | 76 | 24 | 0 |
| 1901-2000 | 13 | 0 | 36 | 1980 | 74 | 26 | 0 |
| 2001-2100 | 14 | 0 | 36 | 2016, 2100 | 74 | 26 | 0 |
| 2101-2200 | 10 | 0 | 40 | 2160 | 76 | 24 | 0 |
| 2201-2300 | 15 | 0 | 32 | 2280 | 75 | 25 | 0 |
| 2301-2400 | 15 | 0 | 36 | 2340, 2400 | 77 | 23 | 0 |
| 2401-2500 | 10 | 0 | 30 | 2448 | 74 | 26 | 0 |
| 2501-2600 | 11 | 1 | 48 | 2520 | 74 | 26 | 0 |
| 2601-2700 | 15 | 0 | 40 | 2640 | 78 | 22 | 0 |
| 2701-2800 | 14 | 0 | 36 | 2772 | 74 | 26 | 0 |
| 2801-2900 | 12 | 0 | 42 | 2880 | 75 | 25 | 0 |
| 2901-3000 | 11 | 0 | 36 | 2940 | 74 | 26 | 0 |
| 3001-3100 | 12 | 0 | 40 | 3024 | 76 | 24 | 0 |
| 3101-3200 | 10 | 0 | 40 | 3120 | 76 | 24 | 0 |
| 3201-3300 | 11 | 0 | 40 | 3240 | 74 | 26 | 0 |
| 3301-3400 | 15 | 0 | 48 | 3360 | 74 | 26 | 0 |
| 3401-3500 | 11 | 0 | 36 | 3420 | 74 | 26 | 0 |
| 3501-3600 | 14 | 0 | 45 | 3600 | 77 | 23 | 0 |
| 3601-3700 | 13 | 0 | 40 | 3696 | 78 | 22 | 0 |
| 3701-3800 | 12 | 0 | 48 | 3780 | 73 | 27 | 0 |
| 3801-3900 | 11 | 0 | 36 | 3840, 3900 | 74 | 26 | 0 |
| 3901-4000 | 11 | 0 | 48 | 3960 | 75 | 25 | 0 |
| 4001-4100 | 15 | 0 | 42 | 4032 | 74 | 26 | 0 |
| 4101-4200 | 9 | 1 | 48 | 4200 | 76 | 24 | 0 |
| 4201-4300 | 16 | 0 | 36 | 4284 | 74 | 26 | 0 |
| 4301-4400 | 9 | 0 | 48 | 4320 | 77 | 23 | 0 |
| 4401-4500 | 11 | 0 | 36 | 4410, 4500 | 77 | 23 | 0 |
| 4501-4600 | 12 | 0 | 40 | 4536, 4560 | 73 | 27 | 0 |
| 4601-4700 | 12 | 0 | 48 | 4620, 4680 | 74 | 26 | 0 |
| 4701-4800 | 12 | 0 | 42 | 4800 | 74 | 26 | 0 |
| 4801-4900 | 8 | 0 | 36 | 4860, 4896 | 76 | 24 | 0 |
| 4901-5000 | 15 | 0 | 36 | 4950 | 77 | 23 | 0 |
| 5001-5100 | 12 | 0 | 60 | 5040 | 75 | 25 | 0 |
| 5101-5200 | 11 | 0 | 36 | 5148 | 74 | 26 | 0 |
| 5201-5300 | 10 | 0 | 48 | 5280 | 77 | 23 | 0 |
| 5301-5400 | 10 | 0 | 48 | 5400 | 74 | 26 | 0 |
| 5401-5500 | 13 | 0 | 48 | 5460 | 75 | 25 | 0 |
| 5501-5600 | 13 | 0 | 48 | 5544 | 74 | 26 | 0 |
| 5601-5700 | 12 | 0 | 40 | 5616, 5670 | 75 | 25 | 0 |
| 5701-5800 | 10 | 0 | 48 | 5760 | 76 | 24 | 0 |
| 5801-5900 | 16 | 0 | 48 | 5880 | 73 | 27 | 0 |
| 5901-6000 | 7 | 0 | 48 | 5940 | 74 | 26 | 0 |
| 6001-6100 | 12 | 0 | 48 | 6048 | 76 | 24 | 0 |
| 6101-6200 | 11 | 0 | 48 | 6120 | 77 | 23 | 0 |
| 6201-6300 | 13 | 0 | 54 | 6300 | 72 | 28 | 0 |
| 6301-6400 | 15 | 0 | 42 | 6336 | 75 | 25 | 0 |
| 6401-6500 | 8 | 0 | 50 | 6480 | 74 | 26 | 0 |
| 6501-6600 | 11 | 0 | 48 | 6552, 6600 | 76 | 24 | 0 |
| 6601-6700 | 10 | 0 | 36 | 6624, 6660 | 73 | 27 | 0 |
| 6701-6800 | 12 | 1 | 56 | 6720 | 76 | 24 | 0 |
| 6801-6900 | 12 | 0 | 48 | 6840 | 76 | 24 | 0 |
| 6901-7000 | 13 | 0 | 48 | 6930 | 74 | 26 | 0 |
| 7001-7100 | 9 | 0 | 48 | 7020 | 76 | 24 | 0 |
| 7101-7200 | 10 | 0 | 54 | 7200 | 74 | 26 | 0 |
| 7201-7300 | 11 | 0 | 40 | 7280 | 74 | 26 | 0 |
| 7301-7400 | 9 | 0 | 48 | 7392 | 76 | 24 | 0 |
| 7401-7500 | 11 | 0 | 42 | 7488 | 75 | 25 | 0 |
| 7501-7600 | 15 | 0 | 64 | 7560 | 73 | 27 | 0 |
| 7601-7700 | 12 | 0 | 40 | 7680 | 76 | 24 | 0 |
| 7701-7800 | 10 | 0 | 48 | 7800 | 77 | 23 | 0 |
| 7801-7900 | 10 | 0 | 36 | 7812, 7840 | 75 | 25 | 0 |
| 7901-8000 | 10 | 0 | 60 | 7920 | 74 | 26 | 0 |
| 8001-8100 | 11 | 0 | 48 | 8064 | 72 | 28 | 0 |
| 8101-8200 | 10 | 0 | 48 | 8160, 8190 | 78 | 21 | 1 |
| 8201-8300 | 14 | 0 | 48 | 8280 | 74 | 26 | 0 |
| 8301-8400 | 9 | 0 | 60 | 8400 | 77 | 23 | 0 |
| 8401-8500 | 8 | 0 | 40 | 8424 | 73 | 27 | 0 |
| 8501-8600 | 12 | 0 | 48 | 8568, 8580 | 74 | 26 | 0 |
| 8601-8700 | 13 | 0 | 56 | 8640 | 78 | 22 | 0 |
| 8701-8800 | 11 | 0 | 48 | 8736 | 75 | 25 | 0 |
| 8801-8900 | 13 | 0 | 54 | 8820 | 75 | 25 | 0 |
| 8901-9000 | 9 | 0 | 48 | 9000 | 76 | 24 | 0 |
| 9001-9100 | 11 | 0 | 50 | 9072 | 76 | 24 | 0 |
| 9101-9200 | 12 | 0 | 48 | 9120, 9180 | 73 | 27 | 0 |
| 9201-9300 | 11 | 0 | 64 | 9240 | 74 | 26 | 0 |
| 9301-9400 | 11 | 0 | 60 | 9360 | 75 | 25 | 0 |
| 9401-9500 | 15 | 0 | 48 | 9450 | 75 | 25 | 0 |
| 9501-9600 | 7 | 0 | 48 | 9504, 9576, 9600 | 75 | 25 | 0 |
| 9601-9700 | 13 | 0 | 48 | 9660 | 76 | 24 | 0 |
| 9701-9800 | 11 | 0 | 48 | 9720 | 73 | 27 | 0 |
| 9801-9900 | 12 | 0 | 54 | 9900 | 78 | 22 | 0 |
| 9901-10000 | 9 | 0 | 40 | 9936 | 77 | 23 | 0 |
The Integers
The integers consist of the positive natural numbers (1, 2, 3, …) the negative natural numbers (-1, -2, -3, ...) and the number zero. The set of all integers is usually denoted in mathematics by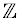 
in blackboard bold, which stands for Zahlen (German for "numbers").
Positive Integers refers to all whole number greater than zero. Zero is not a positive integer. For each positive integer there is a negative integer. Integers greater than zero are said to have a positive “sign”.
The Positive Integers are a subset of the Natural Numbers (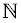
), depending on whether or not 0 is considered a Natural Number. The term Positive Integers is preferred over Natural Numbers and Counting Numbers because it is more clearly defined; there is inconsistency over whether zero is a member of those sets. Zero is not an element of the Positive Integers.
The Positive Integers are symbolized by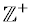 
.
Prime numbers are a subset of the positive integers and are of special interest in Number Theory. Note that the number 1 is not a prime number; i.e., for the set of prime numbers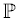 
, all 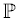> 1. A prime number is a positive integer that has no positive integer divisors except for 1 and itself. Positive Integers that are not Prime Numbers or 1 are Composite Numbers. The number 1 is neither a Prime Number nor a Composite Number.
Algebraic properties of Integers
Like the natural numbers, 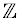is closed under the operations of addition and multiplication; that is, the sum and product of any two integers is an integer. However, with the inclusion of the negative natural numbers and zero, 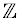(unlike the natural numbers) is also closed under subtraction. 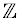is not closed under the operation of division, since the quotient of two integers ( e.g. , 1 divided by 2), need not be an integer.
The following table lists some of the basic properties of addition and multiplication for any integers a , b and c .
| addition | multiplication | |
| closure : | a + b is an integer | a × b is an integer |
| associativity : | a + ( b + c ) = ( a + b ) + c | a × ( b × c ) = ( a × b ) × c |
| commutativity : | a + b = b + a | a × b = b × a |
| existence of an identity element : | a + 0 = a | a × 1 = a |
| existence of inverse elements : | a + (- a ) = 0 | |
| distributivity : | a × ( b + c ) = ( a × b ) + ( a × c ) | |
Ordering
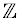is a totally ordered set without an upper or lower bound. The ordering of 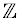is given by
An integer is positive if it is greater than zero and negative if it is less than zero. Zero is defined as neither negative nor positive.
The ordering of integers is compatible with the algebraic operations in the following way:
- if a < b and c < d , then a + c < b + d
- if a < b and 0 < c , then ac < bc
Divisors
A divisor of an integer n, also called a factor of n, is an integer which evenly divides n without leaving a remainder. If x is a divisor of n, it can be written that x|n. This is read as x divides n. It is also said that n is divisible by x, and that n is a multiple of x.
1 and -1 are divisors of every integer, and every integer is a divisor of 0. Numbers divisible by 2 are called even and those that are not are called odd.
The name comes from the arithmetic operation of division : if a/b=c, then a is the dividend, b the divisor, and c the quotient.
Some elementary properties of Divisors are:
- If a|b and a|c, then a|(b+c).
- If a|b and b|c, then a|c.
- If a|b and b|a, then a=b or a=-b.